Color and Learn About the Periodic Table

This exploration is for kids 10 and up, as the colored smilies show. You can learn about the periodic table of the elements with kids from 5th grade up to 12th!

The periodic table of the elements lesson is a chemistry exploration from Layers of Learning Unit 1-13 about elements. Layers of Learning has hands-on experiments in every unit of this family-friendly curriculum. Learn more about Layers of Learning.

The periodic table of the elements is a visual way that chemists have developed to organize the elements of the universe.  With this method elements are grouped next to other elements that are similar.  As the periodic table was being developed there were many undiscovered elements whose presence was predicted based on a blank spot in the chart.  The periodic table is one evidence that the universe is orderly and predictable.

Step 1: Library Research

Before you begin exploring, read a book or two about the periodic table of the elements. Here are some suggestions, but if you can’t find these, look for books at your library about motion, physics, gravity, and friction. The colored smilies above each book tell you what age level they’re recommended for.

As Amazon affiliates, the recommended books and products below kick back a tiny percentage of your purchase to us. It doesn’t affect your cost and it helps us run our website. We thank you!

The Periodic Table: Elements With Style

by Adrian Dingle

Periodic Table

by Sean Callery

Step 2: Periodic Table Exploration

You will need the periodic table printable and colored pencils, crayons, colored pens, or paint.

Start by coloring the families of elements as shown in the example below. Families are elements that have similar properties. They behave in similar ways physically and chemically.

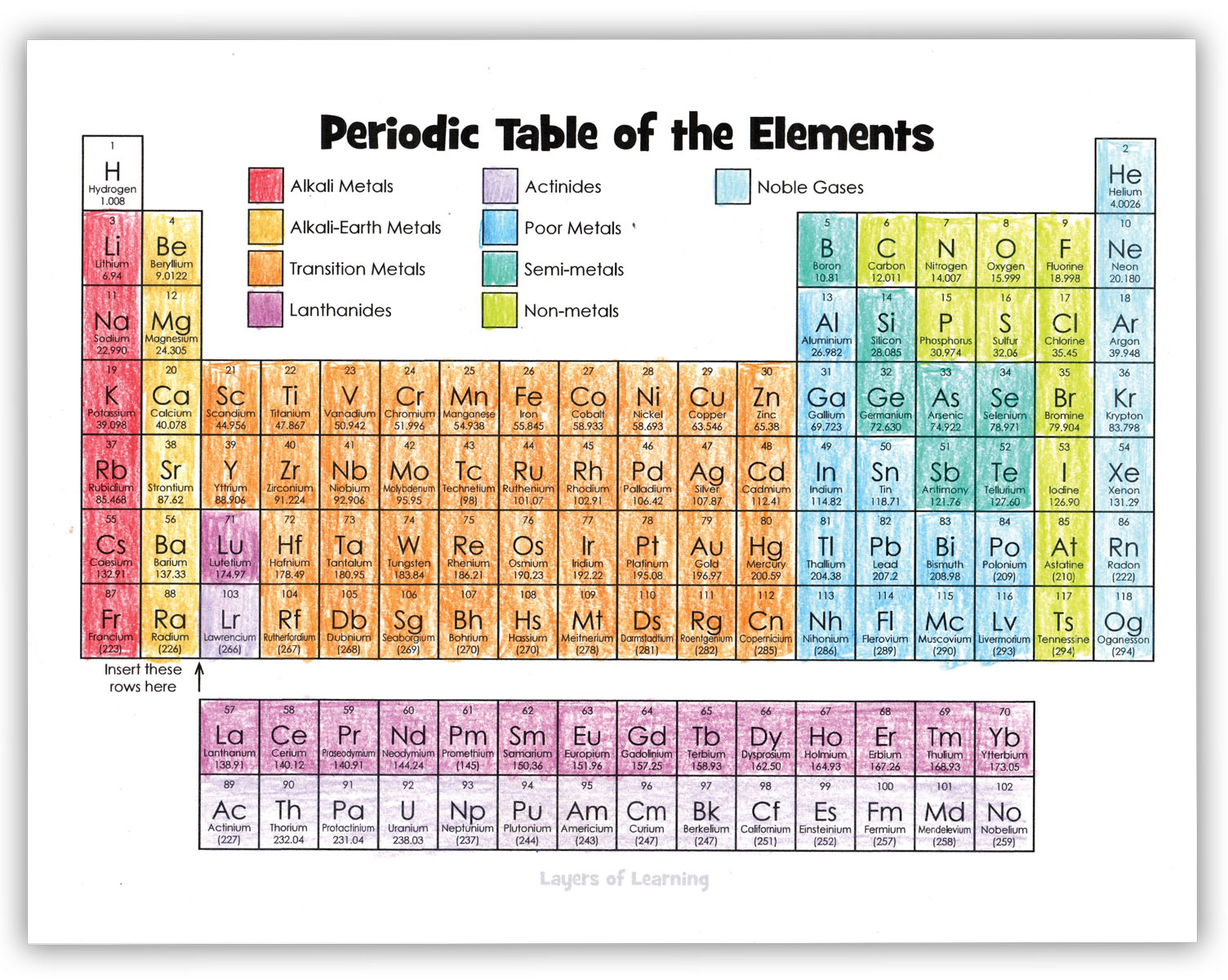
Some Rules of the Periodic Table

Next, learn some of the rules of the periodic table.

Periods run horizontally across the table in rows and the atomic number goes up one as you move from left to right. The atomic number is the number of protons in an atom. The atomic number is the large number at the top of the box for a particular element.

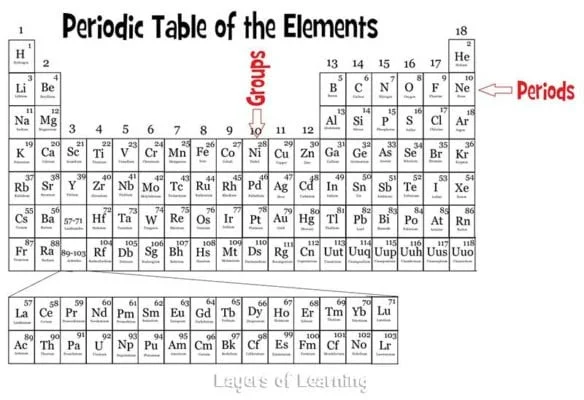
Groups run vertically down the table and all elements in a particular group have the same number of electrons in their outer shell, so they behave in similar ways.  The first group, the Alkali metals, have one outer shell electron.  The second group has two.  Then we skip the dropped down section and go to the group that begins with Boron.  The Boron group has three electrons, and so on up to the noble gases which have eight electrons in their outer shell.

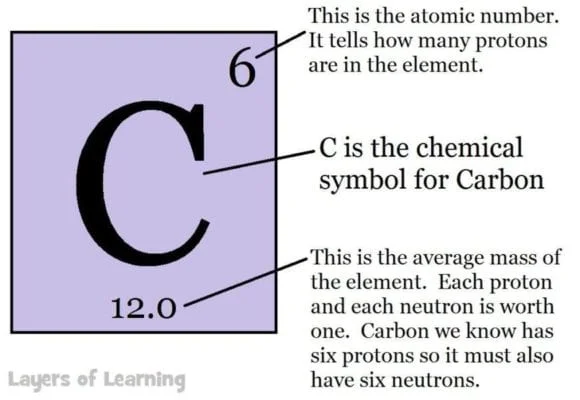
The letters in each box are a symbol for the chemical. The symbol for carbon is C, the symbol for lead is Pb and comes from the Latin for lead which is plumbum.

The number at the bottom of the element’s box is the atomic weight, or total weight of protons, neutrons, and electrons for that element. Hydrogen, which has one proton and one electron has a weight of 1. (The weight of electrons compared to protons and neutrons is negligible and not really counted.)

As you explore the periodic table, you can also play this interactive Build an Atom game to practice constructing atoms based on elements within the periodic table.

Step 3: Show What You Know

After you’ve explained the basic rules of the periodic table, quiz the kids giving rewards for good performance.

• Which family does Xenon (Xe) belong to?
• What is the chemical symbol for gold?
• How many electrons are in the outer shell of Boron (B)?
• Name an element in the same group with Carbon.
• Which element has the chemical symbol Na?
• How many electrons are in the outer shell of the Halogen gasses?

You get the idea. This exercise is not intended to help kids memorize the periodic table, but rather to learn what the symbols mean and how to interpret them, so they can reference the table when they need information later.

Additional Layers

Additional Layers are extra activities you can do or tangents you can take off on. You will find them in the sidebars of each Layers of Learning unit. They are optional, so just choose what interests you.

Additional Layer

People have proposed many alternative ways to organize the periodic table. Here’s one idea.

Read more about the alternative periodic tables that have been proposed.

On the Web

In the Layers of Learning catalog each unit has a list of web sites to explore the topics further.

To learn more about the periodic table of the elements visit https://www.ptable.com/ where you can click on the elements to learn more about them one by one.

To build familiarity, have your kids play an online solitaire game with periodic table element cards.

Famous Folks

Russian chemist and inventor, Dmitri Mendeleev, organized the first periodic table as we know it today.

He even predicted the existence of elements that had not yet been discovered.

Get a Free Unit

Choose between the first unit in each Layers of Learning subject to try for free when you sign up for the newsletter.

We never spam and you can cancel your subscription at any time.

First Name

Please enter your name.

Email Address

Please enter a valid email address.

Sign up for the Newsletter!

Thanks for subscribing! Please check your email inbox and spam folders for a confirmation link.

Something went wrong. Please check your entries and try again.